Repaso desde Medidas hasta Movimiento en 2D

Esta nota todavía está en construcción.

Esta nota es un esbozo y por lo tanto incompleta. Ampliandola ayudarás a mejorar esta página.

Antes de empezar

Este repaso asume que ya has visto las clases de tu profesor de Fisica.

También asume que no has entendido uno o varios temas de tu profesor.

Magnitudes y medidas/unidades

Magnitud física: lo que quiero medir. Ejemplo: tiempo ($t_x$), distancia ($d_x$), masa ($m_x$), temperatura (?). Unidad física: el patrón con lo que comparo la magnitud. Ejemplo: segundo ($s$), metro ($m$), kilogramo ($kg$), kelvin ($K$).

De estas provienen:

• Magnitudes/unidades fundamentales: Distancia ($m$), tiempo ($s$), masa ($kg$), etc. Es una base independiente
• Magnitudes/unidades derivadas: Velocidad ($\frac{m}{s}$), aceleración ($\frac{m}{s^2}$), peso/fuerza ($N$), área ($m^2$), volumen ($m^3$), etc. Deriva de 2 o más unidades fundamentales.

Ejemplo más claro: Con análisis dimensional, la magnitud fundamental sería “distancia” y la unidad “metro” ($m$), o magnitud “tiempo” y la unidad “segundo” ($s$). La magnitud derivada de estas dos por lo tanto sería “velocidad” y su unidad “metros/segundos” ($\frac{m}{s}$).

Otro ejemplo:

“Aumenta cada 2 $\frac{m}{s}$ cada segundo”

a) Velocidad b) Aceleración

Cifras significativas

¿Cómo reportamos la precisión de una medida? En cifras significativas

Pero qué es precisión?

Supongamos que eres Goku peleando contra

Repaso rápido de trigonometría

• Hipotenusa: El lado más largo del triángulo.
• Cateto opuesto: El lado de la vertical, frente al ángulo agudo. (en nuestro caso, $\theta$)
• Cateto adyacente: El cateto de la horizontal, tocando el ángulo agudo.

Porqué un ángulo $\theta$ se puede poner en cualquier lado del triángulo?

No es que se pueda poner en cualquier lado.

Un triángulo rectángulo tiene 3 ángulos: un ángulo recto y ==dos ángulos agudos==.

Eso si, los catetos cambian donde se ubique el ángulo agudo (se escribe con cualquier letra griega, por ejemplo $\alpha$, o en este caso, $\theta$), por ello se dice que los catetos opuesto y adyacente son variables.

Operaciones con triángulos

Venimos entonces con las siguientes operaciones (con sus definiciones formales en paréntesis):

• Obteniendo la hipotenusa: $h$
• $\text{sen}(\theta )$ (en una calculadora $\sin (\theta )$): Cuánto de “vertical” tiene el ángulo. ($\frac{cat.op}{h}$)
• $\cos (\theta )$: Cuánto de “horizontal” tiene el ángulo. ($\frac{cat.adj}{h}$)
• $\tan (\theta )$: La razón entre “vertical” y “horizontal”. ($\frac{cat.op}{cat.adj}$)

¿Una razón?

Nos referimos a una razón como la división entre dos cantidades (digamos, $\frac{6}{8}$), o una relación binaria entre dos cantidades ($6:8$).

Por ejemplo, las operaciones seno y coseno devuelven un ratio (Cuánto de $x$ tiene) mientras que el tangente es una división entre el cateto opuesto y el cateto adyacente.

Esto importa a la hora de invertir las operaciones (fijándonos en la tabla, donde $\theta$ es $44.4$):

Función (ejemplo)	Recibe	Entrega
$\sin (\theta )=0.7$	Ángulo	Ratio
$\arcsin (0.7)=\theta$	Ratio	Ángulo

Unos truquitos

Si quieres dominar estos significados lo más importante sería saber la simplificación de un exponente: $x^2=a^2⟹x=\sqrt[2]{a}$, lo cual se llama radicación.

Por ejemplo en la obtención de la hipotenusa al tener los dos catetos:

$$h^2=c{a}^2+c{o}^2⟹h=\sqrt{c{a}^2+c{o}^2}$$

También puedes mostrar la raíz al pasar el índice al exponente dentro de una unidad de la raiz (básicamente un exponente fraccionario):

$$|x|\equiv \sqrt{x^2}⟹x^{\frac{2}{2}}$$

En la cual $|x|$ es el valor absoluto de $x$.

Tabla de ángulos (importante!)

Esta tabla será importante a la hora de hacer quizes o parciales, dado que están diseñados para no usar calculadora.

Ángulo ($\theta$)	En radianes	$\sin (\theta )$	$\cos (\theta )$	$\tan (\theta )$
$0^{\circ }$	$0$	$0$	$1$	$0$
$30^{\circ }$	$\pi /6$	$1/2$	$\sqrt{3}/2$	$1/\sqrt{3}$
$45^{\circ }$	$\pi /4$	$\sqrt{2}/2$	$\sqrt{2}/2$	$1$
$60^{\circ }$	$\pi /3$	$\sqrt{3}/2$	$1/2$	$\sqrt{3}$
$90^{\circ }$	$\pi /2$	1	0	$\nexists$

Vectores

Antes de comenzar...

En física (lo que he investigado) nos referimos a un escalar/constante a lo siguiente:

• $30\text{ minutos}$
• $5\text{ kilogramos}$
• $10\text{ metros}$

También hay que aclarar que una vez pasado por una función (como $\cos$, $\sin$) su resultado ES ADIMENSIONAL, DEBE DE SER UN NÚMERO

Por lo tanto, un vector es lo siguiente:

“Objeto con una flecha que representa una magnitud con dirección, esta teniendo su sentido”

Estos vectores, se dibujan en el plano cartesiano, y pueden representar, por ejemplo, una fuerza o una velocidad. Tienen un punto de origen y un punto final.

Componente de un vector

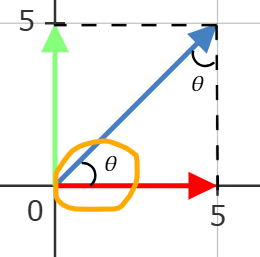
Imaginate que tenemos un vector en un plano cartesiano. El vector empieza en el origen $(0,0)$ y apunta en diagonal tal como se puede ver en el plano:

Llamémosle a este vector $\vec{F}$, siendo $\vec{F}=(5,5)\equiv 5\hat{i}+5\hat{j}$. (A esto se le llama vectores unitarios) Para llegar a la punta azul, debemos de subir 5 unidades hacia arriba y hacia la derecha.

Ahora, imagina que esa flecha proyecta una sombra al apuntarle una linterna. Esa sombra indica en que parte va a estar ubicado la componente. En pocas palabras, es como si hubiera un dominio (componente x) y un rango (componente y) en un vector, solo que en este caso, se usa el valor final del dominio/rango como punto final del componente.

El componente de un vector se escribe como ${\mathcal{V}}_x$ (el eje $x$, en el caso de $\vec{F}$, es 5) y ${\mathcal{V}}_y$ (el eje $y$, en el caso de $\vec{F}$, también es 5).

Se obtiene restando las coordenadas del punto final (${\vec{F}}_{bx}$) por las coordenadas del punto inicial (${\vec{F}}_{ax}$): ${\vec{F}}_x={\vec{F}}_{bx}-{\vec{F}}_{ax}$

Módulo/magnitud de un vector

Si el vector tiene un punto origen $(0,0)$ y un punto final $(5,5)$ veremos que forma un triángulo rectángulo:

Usando el Teorema de Pitágoras podemos obtener formalmente el módulo de un vector, en este caso $\vec{F}$, dando como resultado $7.07$. Este es el tamaño real de la flecha. Se escribe como $|\vec{F}|$.

Dirección/ángulo de un vector

Ya tenemos el punto inicial, el punto final, las componentes y la magnitud. Ahora nos falta el ángulo, es decir, la dirección de nuestro vector… Y volvemos al inicio de nuestro repaso rápido de trigonometría: $\sin ,\cos \text{y}\tan$.

Para obtener el ángulo de nuestro vector cuando ya tengo las dos sombras (el componente ${\vec{F}}_x$ y el componente ${\vec{F}}_y$), usamos la tangente:

$\tan (\theta )=\frac{\text{Opuesto (La sombra en y o sombra de pared)}}{\text{Adyacente (La sombra en x o sombra de piso)}}$

En pocas palabras, y traducido a nuestro vector: $\tan (\theta )\equiv \frac{{\vec{F}}_y}{{\vec{F}}_x}=\frac{5}{5}$

Pero en el triángulo anterior aparece que el cateto adyacente es $y$!

Como se dijo en esa nota, un ángulo se puede poner en cualquier lado. En este caso estamos usando el ángulo inferior para evitar confusiones, por lo que el cateto adyacente sería ${\vec{F}}_x$ (la flecha roja) y nuestro cateto opuesto sería ${\vec{F}}_y$ (la recta entrecortada). Ya volveremos a esto más tarde.

Pero… ¿no nos da esto un ratio? Si, nos da 1, que es nuestro ratio. Pregúntate ahora, qué ángulo tiene una tangente con valor 1? ¿No te suena? ${\tan }^{-1}(1)=45^{\circ }\equiv \theta$ Usando la arcotangente. Ya tenemos nuestra dirección (o ángulo) de nuestro vector. Ahora podemos saber más ecuaciones.

En otro caso, cómo se cual es el ángulo agudo superior/inferior?

Supongamos que en nuestro caso hallamos la ${\tan }^{-1}(\frac{4}{5})\approx 38.66$ de nuestro ángulo inferior. Para saber el ángulo superior solo basta usar el principio del ángulo recto:

$$90-38.66\equiv 90-\theta ⟹39^{\circ }$$

Dándonos un resultado de $51.34^{\circ }$. Ese es el ángulo superior.

O en otros casos donde sea mayor que 90° (el resto es facil de hacer si sabes las propiedades de un triángulo rectangulo): $180-\theta$

O… si eres un flojo wn… Puedes invertir la fracción de la tangente…

$$\begin{array}{c}{\tan }^{-1}(\frac{5}{4})\approx 51.34^{\circ }\\ {\tan }^{-1}(\frac{4}{5})\approx 38.66^{\circ }\end{array}$$

El punto es, aprende bastante trigonometría y teclas.

Operaciones de vectores

Antes de empezar... ( IMPORTANTE)

Antes de pasar a las operaciones, necesitamos dominar lo contrario: cuando el problema te da la flecha con solo la magnitud y tú tienes que hallar las sombras/componentes.

Vamos a hacer un ejercicio rápido, sin hacer trampa (no te devuelvas). Toma esta situación:

Estás arrastrando una maleta en el aeropuerto. La maleta no está totalmente pegada al suelo. Se tira del mango en diagonal aplicando una fuerza de 20 Newtons en un ángulo de 30° sobre la horizontal. Qué parte de la fuerza lo mueve y que parte lo levanta?

Respuesta del ejercicio

El ejercicio te da una pista: sobre la horizontal.

Por lo tanto usamos la siguiente ecuación:

$${\vec{F}}_x=|\vec{F}|\cdot \cos (30)$$

En la que $|\vec{F}|$ implica la magnitud y ${\vec{F}}_x$ implica el cateto adyacente. Repetimos lo mismo con el cateto adyacente y tenemos de resultado:

$${\vec{F}}_x\approx 17.32\&{\vec{F}}_y=10$$

Todo eso solo usando la tabla y las funciones con triángulos.

Suma y resta

La suma y resta de dos vectores, es la suma o resta de las componentes de dos o más vectores.

$$\begin{array}{c}\vec{A}+\vec{B}=({\vec{A}}_x+{\vec{B}}_x,{\vec{A}}_y+{\vec{B}}_y)\\ \vec{A}-\vec{B}=({\vec{A}}_x-{\vec{B}}_x,{\vec{A}}_y-{\vec{B}}_y)\end{array}$$

Ejemplo

Imagina que tu y un grupo están jugando a la cuerda.

• Tu intentas tirar lo más que puedas de la cuerda: $\vec{A}=(4,5)$.
• Tu amigo te intenta ayudar, pero es demasiado flojo: $\vec{B}=2\hat{i}+1\hat{j}$.

Para encontrar la fuerza total que siente la cuerda con la fuerza tuya y la de tu amigo, se deben de sumar las componentes de los vectores.

$$\vec{R}\equiv \vec{A}+\vec{B}=({\vec{A}}_x+{\vec{B}}_x,{\vec{A}}_y+{\vec{B}}_y)$$

Lo que nos da como resultado $\vec{R}$:

La ley del paralelogramo

Hay un procedimiento gráfico sencillo que permite hallar la suma de dos vectores. Esta es la ley del paralelogramo y establece que si dos vectores comparten un mismo punto de origen se completan formando un paralelogramo, su suma es la diagonal que sale de ese punto de origen.

Lo mismo pasa cuando uno de tus oponentes tira demasiado fuerte, tanto que desequilibra a tu equipo ($\vec{C}=(-8,-4)$).

$$\begin{array}{c}\vec{S}=\vec{R}-\vec{C}=(8(-\hat{i})+6\hat{i},4(-\hat{j})+6\hat{j})\\ =(6\hat{i}-8\hat{i},6\hat{j}-4\hat{j})\\ =-2\hat{i}+2\hat{j}\end{array}$$ Nota: solo se ordenaron las variables de la operación, el resultado no cambia.

Producto

Constante ($a$) $\cdot$ Vector

Si el problema dice: “La fuerza se duplica” ($2\cdot \vec{A}$), es tan sencillo como multiplicar ese 2 por cada componente.

Si tu vector era $\vec{A}=(4,5)$:

$$2\cdot \vec{A}=(2\cdot 4,2\cdot 5)=(8,10)$$

En pocas palabras, la flecha se hace el doble de larga, pero mantiene la misma dirección.

Producto Escalar ($A\cdot B$)

El resultado es y será siempre un número.

Producto Vectorial ($A\times B$)

El resultado es y será siempre un vector.

Movimiento

Antes de empezar.

PD: La siguiente nota es lo que recuerdo que dijo el profesor en la clase. Es solo una opinión.

En este bloque, no va a ser fácil aprenderse las ecuaciones, y lo mejor, es solo aprenderse lo básico, ya que para encontrar una ecuación deseada se hace el análisis de un ejercicio usando cosas básicas. Aún así aprendas las ecuaciones de MRU (Movimiento 1D), igual las conseguirás sabiendo lo básico, y trigonometría.

Hagan ejercicios!!! Sobre todo practicar trigonometría.