Intervalos y puntos del plano cartesiano

Esta nota todavía está en construcción.

Esta nota es un esbozo y por lo tanto incompleta. Ampliandola ayudarás a mejorar esta página.

(Pre-introducción) Notación de conjuntos

Por extensión.

Sabemos que, $a=\{Juan,Carlos,Jose\}$ es un conjunto donde $a$ , por ejemplo, es el “Nombre”, es por extensión.

Por compresión.

Sabemos que, $B=\{x|xesEstudiante\}$ es un conjunto dónde $B$ es la compresión, quiere decir que describe una propiedad, en este caso, "$xesEstudiante$".

Intervalos

Un intervalo es un conjunto de 2 variables en la que $a$ y $b$ pertenecen al conjunto de los números reales $\mathbb{R}$, definido cómo:

$$a,b\in \mathbb{R}$$

Esto puede tener tanto su forma abierta en paréntesis ”()”, como su forma cerrada usando corchetes ”[]”, por lo tanto podemos ver 4 variantes en pares ordenados:

$$\begin{array}{c}(a,b)=\left\{x\in \mathbb{R}|a<x<b\right\}\\ [a,b]=\left\{x\in \mathbb{R}|a\le x\le b\right\}\\ (a,b]=\left\{x\in \mathbb{R}|a<x\le b\right\}\\ [a,b)=\left\{x\in \mathbb{R}|a\le x<b\right\}\end{array}$$

Ejemplos

Por ejemplo, tenemos los intervalos $(5,7)$ , $[5,7]$ y $(5,7]$. Sabemos que estos son conjuntos por comprensión, los cuales conforman a $x\in \mathbb{R}$. Por lo tanto:

$$\begin{array}{c}(5,7)=\left\{x\in \mathbb{R}|5<x<7\right\}\\ [5,7]=\left\{x\in \mathbb{R}|5\le x\le 7\right\}\\ (5,7]=\left\{x\in \mathbb{R}|5<x\le 7\right\}\end{array}$$

Cabe aclarar que $[-\infty$ y $\infty ]$ como conceptos no existen, solo existen sus contrapartes abiertas, siendo $(-\infty$ y $\infty )$.

Un poco de graficación (maluca)

Supongamos que tenemos el intervalo $(2,3)$, hariamos lo siguiente:

----------2(////////)3----------⇒ | siendo este $2\le x\le 3$

¿Cómo hacemos ahora usando $\infty$? En este caso vamos a usar $(-\infty ,2)$.

////////////////////)3----------⇒ | siendo este $2\le x\le 3$

Operaciones de conjuntos.

Unión ($\cup$)

Una unión ($\cup$) es cuando tenemos 2 conjuntos por extensión (en este caso $M$ y $N$) los cuales forman otro conjunto conformado con los elementos que pertenezcan a $M$ ó a $N$, tal como se puede ver en la imagen:

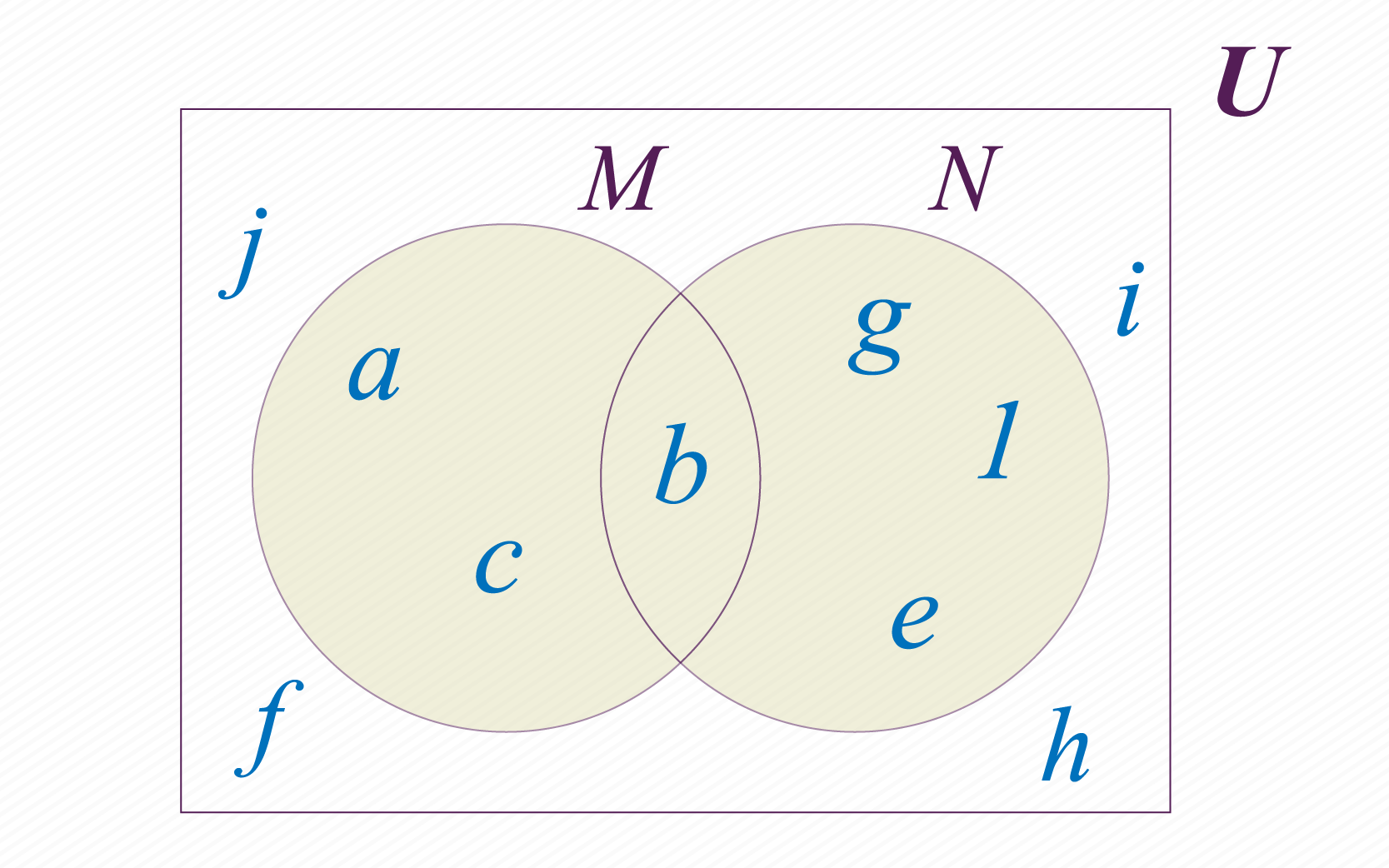
A este nuevo conjunto se le llamaría $M$ y $N$, pero usando el símbolo de unión ($\cup$): $M\cup N$. Este conjunto por comprensión estaría declarado de la siguiente forma:

$$M\cup N=\left\{x|x\in M\acute{o}x\in M\right\}$$

En este caso al preguntarnos cuales están en ese conjunto por comprensión, debemos de saber que la condición es que $x$ debe de estar en $M$ o $N$. Por lo tanto, obtendríamos como resultado: $M\cup N=\left\{a,c,b,g,e,1\right\}$.

Intersección ($\cap$)

Una intersección ($\cap$) es un conjunto por comprensión conformado por los elementos que nuestros conjuntos $M$ y $N$ tienen en común, tal como se puede ver en la imagen:

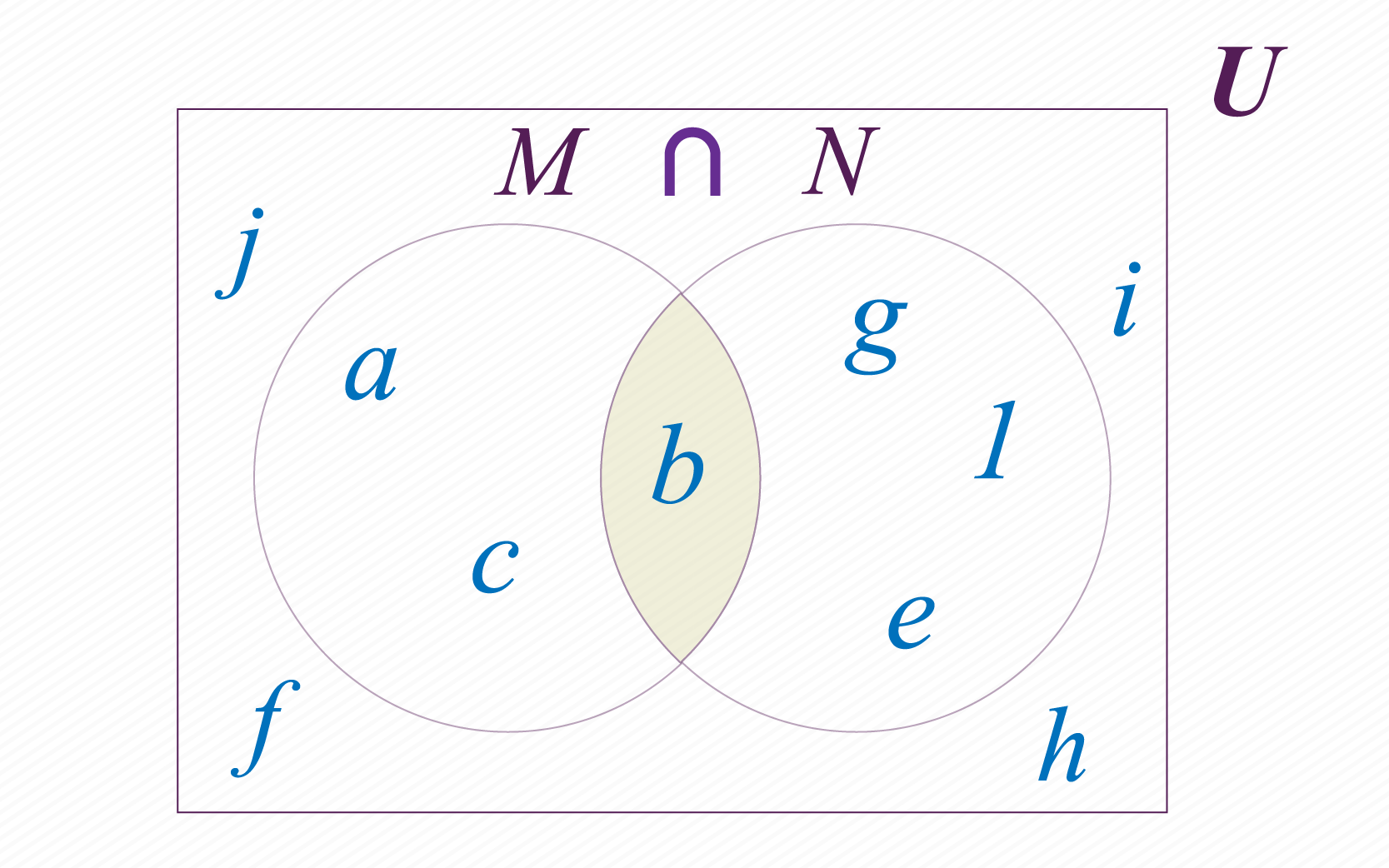
Este conjunto por comprensión se declara de la siguiente forma:

$$M\cap N=\left\{x|x\in Myx\in M\right\}$$

En este caso, la condición es que $x$ debe de estar en $M$ y $N$. Por lo tanto, obtendríamos como resultado: $M\cap N=\left\{b\right\}$.

Diferencia ($-$)

La diferencia (Expresada de dos formas: $M-N$ o $M/N$) es un conjunto por comprensión en el que los elementos de un conjunto no están en el otro conjunto, tal como se puede ver en la imagen.

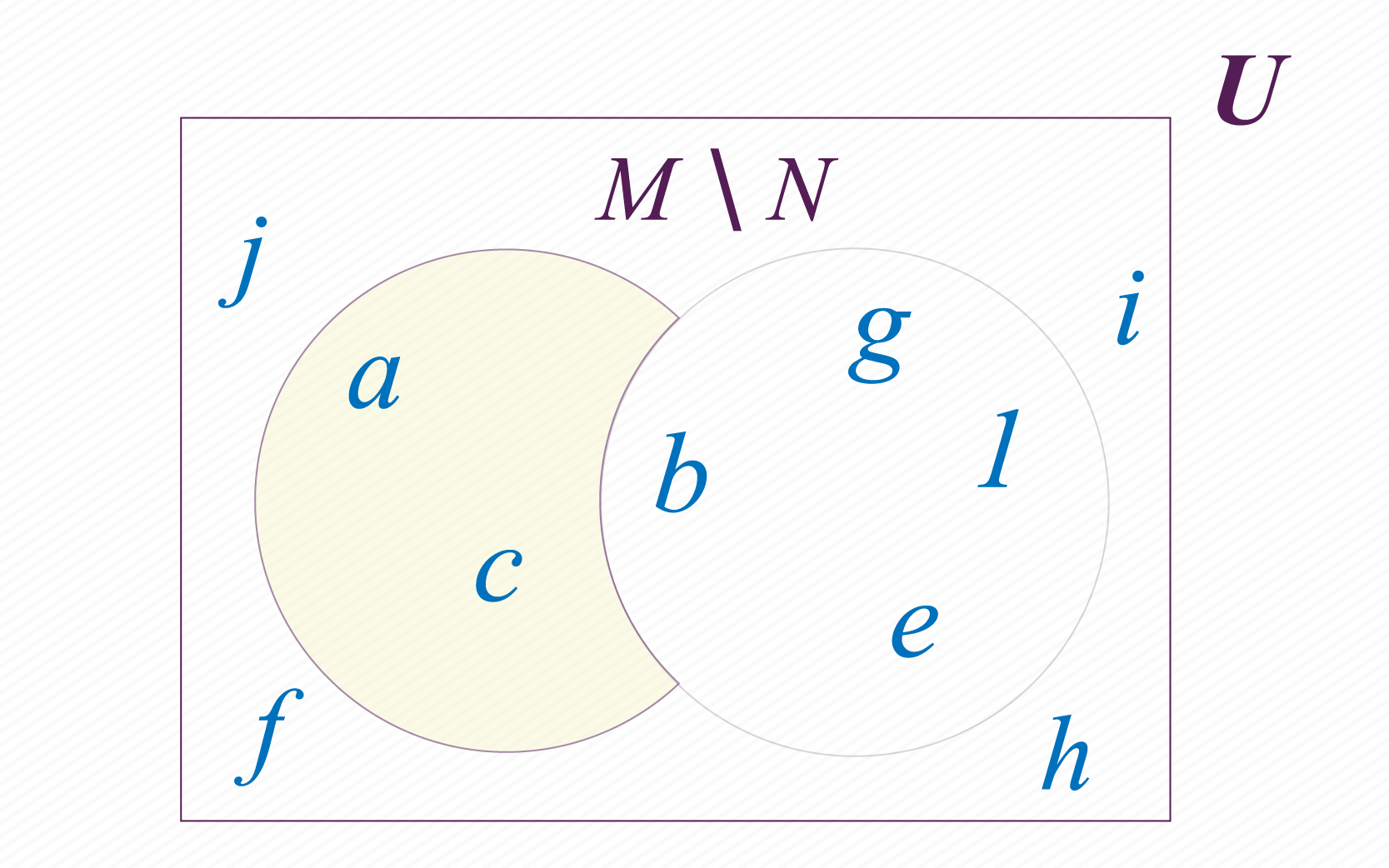
x[^1]

IMPORTANTE: $\varnothing$ significa un conjunto que no tiene nada. Es decir, absolutamente nada: $\varnothing =\left\{\right\}$ .

Complemento o contención ($\subset$)

Puntos del plano cartesiano

Un plano cartesiano es un espacio con dos (o tres) rectas perpendiculares el cual se utiliza para asignarle una ubicación a cualquier punto en un plano.

Sabemos que un punto del plano cartesiano es representado por un par $(x,y)$, donde $x$ es en la recta horizontal o de las abscisas y $y$ en la recta vertical o de las ordenadas.

Este plano cartesiano tiene un origen o punto cero, el cual identifica el punto 0: representa una escala numérica que será positiva o negativa de acuerdo a la dirección del punto.

Este plano cartesiano tiene también 4 cuadrantes, 4 áreas formadas por la unión de las dos rectas anteriormente mencionadas; estos cuadrantes son enumerados con números romanos:

• Cuadrante I: la abscisa ($x$) y la ordenada ($y$) son positivas.
• Cuadrante II: la abscisa ($x$) es negativa y la ordenada ($y$) positiva.
• Cuadrante III: tanto la abscisa ($x$) como la ordenada ($y$) son negativas.
• Cuadrante IV: la abscisa ($x$) es positiva y la ordenada ($y$) negativa.